Pentagon Formula Surface Area

Most of the common type of pentagon that is followed during construction as well as a regular polygon having all equal sides and angles.

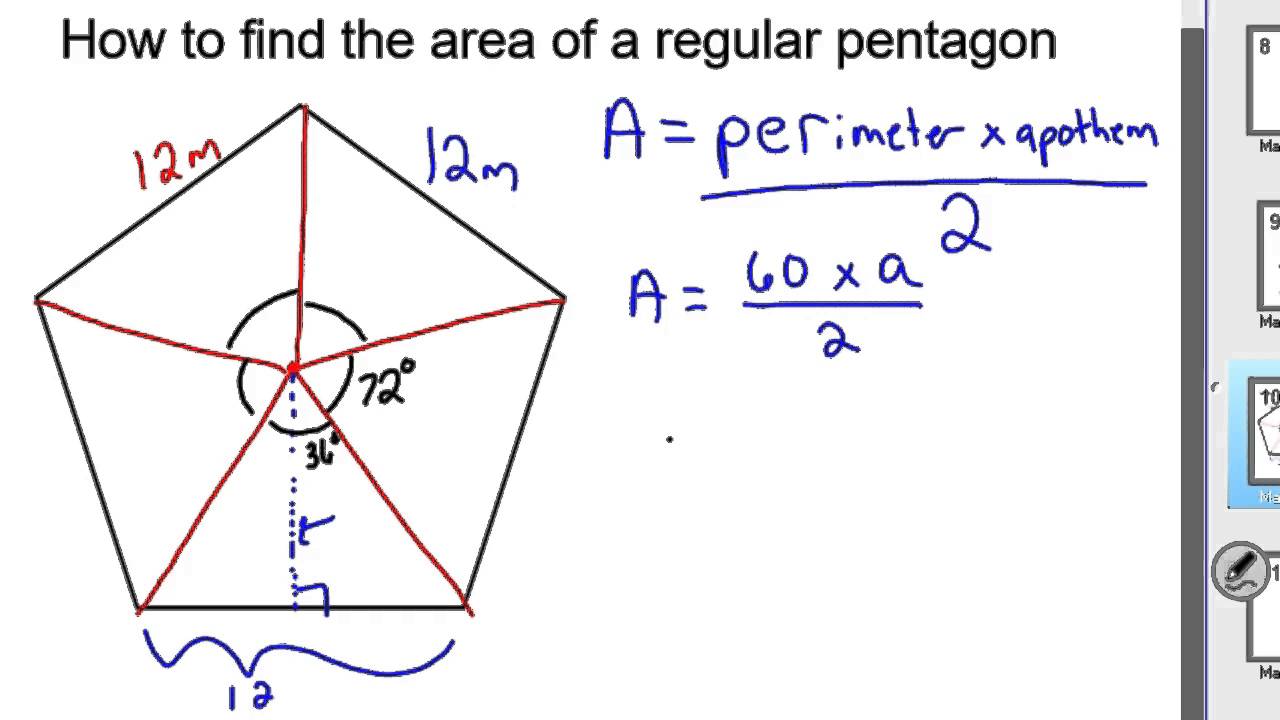
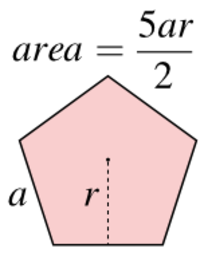
Pentagon formula surface area. The surface area is the areas of all the parts needed to cover the can. Given s 10 cm a 5 cm area of a pentagon a 5 2 s a a 5 2 10 5 cm 2 125 cm 2. Then draw 5 lines from the center 1 to each corner so you have 5 triangles. That s the formula for area of a circle pi r 2.

An online surface area of a pentagon calculator to calculate the pentagonal surface area. It can be sectored into five triangles. A polygon with five sides is called a pentagon. The formula to find the surface area of the pentagonal prism is given by surface area of pentagonal prism 5ab 5bh square units.

This is a prism where the ends are regular pentagons. That s the top the bottom and the paper label that wraps around the middle. The surface area is the area that describes the material that will be used to cover a geometric solid shape. Next find the area of 1 triangle by using the formula area base height where the base is the side of the pentagon and the height is the apothem.

You can find the surface area by knowing the side length and apothem length. Where s is the side of the pentagon and a is the apothem length. Regular pentagons have 5 sides of equal length. This surface area calculator pentagon works based on the inputs of side length and apothem length.

Pentagon is the five sided polygon with five sides and angles. It can be a simple polygon or a self intersecting one. In this lesson we find a general formula for the surface area of a pentagonal prism. To calculate the area the length of one side needs to be known.

Also the length of a line from the middle of a side to the middle of the pentagon is needed. Surface area 2 pi r 2 2 pi r h in words the easiest way is to think of a can. The surface area is the total surface area that the object occupies. Area of a pentagon.

The page provides the pentagon surface area formula to calculate the surface area of the pentagon. The area of a pentagon formula in mathematics can be given as. Example questions using pentagon area formula. It has 5 sides and 5 equal angles.

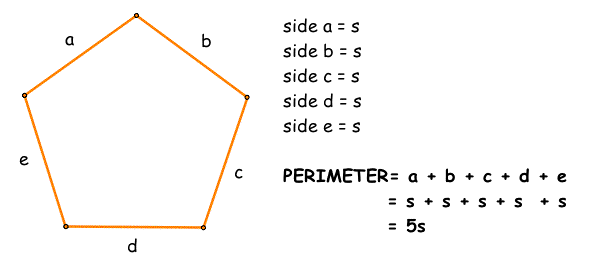
Finally multiply that result by 5 to get the pentagon s area. You can find the area of the top or the bottom. The area is defined as the space occupied within boundaries of the pentagon. A regular pentagon means that all of the sides are identical and all angles are the same as each other.

Here we will discuss the area of a pentagon formula. In a regular pentagon the five sides are equal in length and the internal angles are equal 108 0 the exterior angles are 72 0 in an irregular pentagon this is not the case the sides may not be equal and the angles can be different.